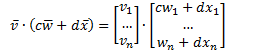Lec 4 - Subspace & Dot Product

Wednesday, January 11, 2012

9:26 AM

Recall:





 

 

Definition



 

 

 

 Theorem: (Subspace Test)

 





 

Proof:

 



Properties 1 and 6 are what is being checked.





 

Note: Our proof shows that any set that does NOT contain the zero vector is NOT a subspace.

 

Eg.





 

Eg.





 





 









=0

Property 4 holds true.

 



 













 



 

Note:







 

Eg.





 



 





 

 

 Dot Product

 

Definition



 



Note: The result of the dot product is a scalar, NOT a vector.

 

Eg







 



 

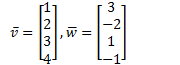
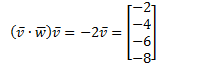
 Theorem (Properties of Dot Product)

 



 

1. 

 

2. 

 

3. 

 

Proof:



 

1. 



 

2. 





 

3. 









Q.E.D.

 

 

Definition



 

Eg.





 

Definition



 

 

 Theorem: (Property of Norms)

 



 

1. 

 

2. 

 

3. 

 

4.